Think DSP Chapter 4: Noise

In my ongoing celebration of DSP month, I am posting excerpts from Think DSP, my new introduction to Digital Signal Processing.  Here are links to the previous installments:

Chapter 1
Chapter 2
Chapter 3

Today's installment is Chapter 4: Noise.  Here's how it starts:

In English, “noise” means an unwanted or unpleasant sound. In the context of digital signal processing, it has two different senses:

1. As in English, it can mean an unwanted signal of any kind. If two signals interfere with each other, each signal would consider the other to be noise.
2. “Noise” also refers to a signal that contains components at many frequencies, so it lacks the harmonic structure of the periodic signals we saw in previous chapters.

This chapter is about the the second kind.

Chapter 4 took a while for me to get organized, because I was tempted to start with "white noise", until I realized that I could not explain what white noise is without getting myself tangled up.  It is easy to generate white noise, but not easy to explain why it is "white".

It made more sense (to me, at least) to start with uncorrelated, uniform (UU) noise and then explore the spectral structure.  What we discover is that UU noise has equal power at all frequencies, on average, and that's why it's called "white".

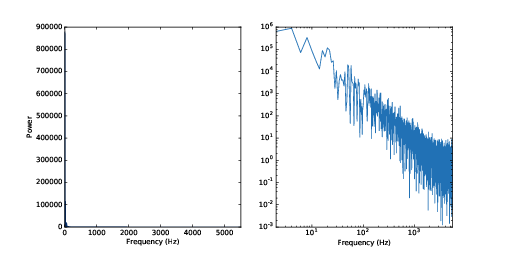
Here's the power spectrum of a segment of UU noise.

It looks like the same power at all frequencies, on average, but it's pretty noisy.  The picture is clearer if we compute the cumulative sum of power:

That smooths out the noise and makes the "whiteness" obvious.

The chapter also presents Brownian noise (aka "red noise") and pink noise, wrapping up this this figure, which shows the power spectrums for red, pink, and white noise on a log-log scale:

You can see the examples from Chapter 4 (and listen to them) in this IPython notebook.

And if you can't wait for Chapter 5, you might be interested in this notebook, which presents the phenomenon of the Missing Fundamental.